Taming COVID-19 Statistics to Reflect Happiness Score Metrics

Permissions

Place an X in the appropriate bracket below to specify if you would like your group's project to be made available to the public. (Note that student names will be included (but PIDs will be scraped from any groups who include their PIDs).

• [X] YES - make available
• [ ] NO - keep private

Overview

In responding to the global pandemic caused by COVID-19, most countries have implemented different strategies to protect its people's health. Their attitude in responding this pandemic may partially represent the government's general attitude to its people. The efforts in vaccinations are a common and leading protection strategy adapted by most countries. In this project, we make use of the vaccination/death data by country, and explore the relationship between the set of {nation-wide onset date of vaccination, average new vaccination/death rate across different time spans}, and various metrics of happiness score in 2021. In particular, we are trying to figure out to what extent our independent varibles, namely all COVID-19 related data, are correlated to these metrics (i.e. social support, healthy life expectancy, perception of corruption, and generosity) of happiness scores. Throughout our careful analysis, we yielded the conclusion that while some of the metrics don't significantly correlate with COVID data, such as perception of corruption and generosity, there does exist a significant correlation for social support and healthy life expectancy against our COVID-19 data representation. Further, in terms of COVID-19 data themselves, a higher average new vaccination time doesn't necessarily bring a decreasing trend in average new death rate globally, and an early onset of vaccination shows a negative correlation versus death rate in developed countries, and ironically a positive correlation versus death rate in developing countries.

Names

• Colin Wang
  • ziw029@ucsd.edu
• Luning Yang
  • l4yang@ucsd.edu
• Weiyue Li
  • wel019@ucsd.edu
• Yuru Zhou
  • yuz101@ucsd.edu

Research Question

How the onset of vaccination, the vaccination rates, and the death rate in a country are related to the happiness score of that country?

Background & Prior Work

In response to the rapid spreading of COVID-19, many countries have implemented social distancing, mandatory quarantine, and reopening guidance measures to reduce the rate of transmission. Therefore, many people’s lifestyles have been changed greatly due to the restricted rules enforced by the government. They were forced to work remotely from home, limited to certain activities, and lived in fear of the virus. The skyrocketed infection rate and death rate not only tolls on people physically but also mentally. In addition, the resulting economic recession from the COVID-19 pandemic negatively impacted people’s mental health. People experience feelings of stress, frustration, anger, anxiety, or loneliness. According to the recent research of “The Implications of COVID-19 for Mental Health and Substance Use” (reference 1), it showed that 4 in 10 adults in the U.S have reported anxiety and depressive disorder.

As such, everyone in the world is waiting for a vaccine to defeat the COVID-19 pandemic, hoping it will bring life back to normalcy. Hence, we are curious to investigate the relation between these three factors: onset of the vaccination, increasing rate of the vaccination, and the death rate, with the different metrics of happiness score (social support, healthy life expectancy, generosity, and percepections of corruption) of the countries. We want to discover how the degree of importance a country attaches to vaccines and the speed at which they are popularized will affect the death rate of the COVID-19 and therefore impact the people's happiness level of the country.

There have been studies on the relationship between the COVID-19 pandemic and the different metrics of happiness score of the country. The World Happiness Report conducted research on “Happiness, trust, and deaths under COVID-19” , which compares the overall life evaluations and measures of positive and negative emotions of different countries in 2020 with the data for 2017-2019 before the COVID-19 (reference 2). The research reported life evaluation scores in that country based on its average income, life expectancy, and four social factors. The researchers have compared the rankings of happiness (average life evaluation) in different countries based on the 2020 survey compared to those in 2017-2019, and the study found that COVID-19 has led to a modest change in the overall rankings (reference 2). There is an insignificant difference in the overall average happiness score from 5.81 in 2017-19 to 5.85 in 2020 (reference 3).

Even though the study revealed that there is no significant difference in the overall happiness score before the COVID-19 and after it, it didn't investigate how the happiness score fluctuates with the onset of the vaccination, the increasing injection rate of the vaccination, and the death rate of the COVID-19. The goal of our project is to use the data with a detailed time frame to investigate how the happiness score changes over time along with these three crucial factors. Through analyzing and visualizing the data with time spans, we hope to determine whether there are clear relationships between these three variables and the happiness score, and therefore further investigate how they are related.

References (include links):

• 1) https://www.kff.org/coronavirus-covid-19/issue-brief/the-implications-of-covid-19-for-mental-health-and-substance-use/

• 2) https://worldhappiness.report/ed/2021/happiness-trust-and-deaths-under-covid-19/

• 3) https://www.economist.com/international/2021/03/20/the-pandemic-has-changed-the-shape-of-global-happiness

Hypothesis

Hypothesis:

An earlier onset and a faster increasing rate of vaccination, which possibly correlates with a lower death rate over time, result in a potentially higher happiness score.

Defense:

• 1) It intuitively makes sense that the earlier the onset of COVID-19 vaccination, the earlier the general public of a country is protected from the virus, which contributes to a decreasing death rate.

• 2) It intuitively makes sense that when the death rate of a country is low, people would experience less stress from the threats of death, which implicitly increases the happiness score of that country.

Dataset(s)

• Dataset Name: Data on Covid-19 (coronavirus) by Our World in Data
• Link to the dataset: https://covid.ourworldindata.org/data/owid-covid-data.csv
• Number of observations: 17267
• Description: This dataset includes information on daily vaccinations and daily death of of COVID-19 around the world. More specifically, this dataset includes information on daily vaccinations, and statistics of people who are fully vaccinated, not fully vaccinated, total_deaths, and new_deaths. Each observation represents the vaccination progress and the death counts for a specific country at a specific time span.

• Dataset Name: World Happiness Report 2021
• Link to the dataset: https://www.kaggle.com/ajaypalsinghlo/world-happiness-report-2021
• Number of observations: 149
• Description: The happiness scores and rankings use data from the Gallup World Poll . The columns following the happiness score estimate the extent to which each of six factors – economic production, social support, life expectancy, freedom, absence of corruption, and generosity.

• Dataset Name: Population by Country - 2020
• Link to the dataset: https://www.kaggle.com/tanuprabhu/population-by-country-2020
• Description: Countries in the world by population in 2020. The population data for each country include Net change, Yearly change, and Density.

We are planning on joining the death dataset with the vaccination progress and population dataset. Then we calculate the rate of death and vaccination at a certain time interval to summarize this time-series data by each country. Finally, with the summarized data, we join it by the world happiness report to do EDA and analysis for possible correlations.

Setup

First, let's configure the IPython notebook display and import (install) all dependencies required to run this notebook. If some packages are missing, pip will automatically install them. After the pip install is done, restart the kernel, rerun the cells in the setup, and you are ready to go! The setup should take longer time to finish the first time you run it due to package installation and dataset download. The dataset will be cached locally so you won't need to download them again after the first time.

%%javascript
IPython.OutputArea.auto_scroll_threshold = 99999;
IPython.OutputArea.prototype._should_scroll = function(lines) {
    return false;
}

import warnings

# Initialization configurations for better visualization effects
%matplotlib notebook
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:70% !important; }</style>"))

try:
    # Data Cleaning / EDA Suite
    import numpy as np
    import pandas as pd
    import matplotlib.pyplot as plt
    import matplotlib.animation as animation
    import matplotlib.style as style
    import seaborn as sns
    import geopandas as gpd
    import altair as alt
    import plotly.express as px
    from celluloid import Camera

    # Tools for building the dataset locally
    import os
    import glob
    import json
    import shutil
    import opendatasets as od

    # Tools for statistical analysis
    from sklearn.decomposition import PCA
    from sklearn.metrics import mean_squared_error, r2_score, normalized_mutual_info_score
    from sklearn.linear_model import LinearRegression
    from sklearn.preprocessing import OneHotEncoder, RobustScaler
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.mixture import GaussianMixture
    from sklearn.svm import SVR
    from sklearn.manifold import TSNE
    import patsy
    import statsmodels.api as sm
except:
    warnings.warn('Missing packages detected. pip is attempting to install all missing dependencies. After this is finished, please rerun this cell', UserWarning)
    !pip install -r requirements.txt

# disable warnings for better visualzation
warnings.filterwarnings('ignore')

pd.set_option('display.max_columns', 8)

The below script will get you all the dataset needed to run this notebook. Make sure you have your kaggle.json ready (see README.md for more details).

# set force_reset = True if you want to rebuild the dataset
def create_dataset(force_reset=False):
    # all the data will be stored locally under the data directory
    data_path = 'data'
    if not os.path.exists(data_path):
        os.makedirs(data_path)
    # make sure we have 3 files in the data folder
    if len(glob.glob('data/*.csv')) != 3 or force_reset:
        try:      
            shutil.rmtree('./owid-covid-data')
            shutil.rmtree('./world-happiness-report-2021')
            shutil.rmtree('./population-by-country-2020')
        except:
            pass
        
        try:
            kaggle = json.load(open('kaggle.json'))
        except:
            print("Make sure your kaggle.json is correctly configured")
        
    # download all of the dataset
        od.download('https://covid.ourworldindata.org/data/owid-covid-data.csv')
        od.download('https://www.kaggle.com/ajaypalsinghlo/world-happiness-report-2021')
        od.download('https://www.kaggle.com/tanuprabhu/population-by-country-2020')
    
    # rename the csv files and save them into the data folder
        os.rename('./owid-covid-data.csv',
                  './data/owid-covid-data.csv')
        os.rename('./world-happiness-report-2021/world-happiness-report-2021.csv', 
                  './data/world_happiness.csv')
        os.rename('./population-by-country-2020/population_by_country_2020.csv',
                  './data/population.csv')
                  
        shutil.rmtree('./world-happiness-report-2021')
        shutil.rmtree('./population-by-country-2020')
    else:
        # if all datasets exist, skip the data preparation
        print("Use Cached Data")
    return True

# create the dataset
create_dataset()

# read all the datasets from the local data folder and save them as seperate Pandas DataFrames
vac_and_death = pd.read_csv('data/owid-covid-data.csv')
happiness = pd.read_csv('data/world_happiness.csv')
population = pd.read_csv('data/population.csv')

Use Cached Data

Data Cleaning

For the first dataset, we decide to extract the information related to how people are vaccinated and the death information in each country. total_vaccinations, people_vaccinated, people_fully_vaccinated, new_vaccinations, and new_vaccinations_smoothed decribe the vaccinated population in each country, while total_deaths and new_deaths decribe how many people die each date and the death increase. For the second dataset, Country name is kept for merging the datasets. We select Social support, Healthy life expectancy, Freedom to make life choices, Generosity, Perceptions of corruption because these are resonable metrics of happiness within these countries. Country (or dependency) is kept for merging for the third dataset. We keep Population (2020), Density (P/Km²), and Med. Age as a description of the overall population in a particular country. We started with the happiness dataset and we merged it with the population dataset, because our target variable is happiness. Using the merged result, we then further merged it with the vaccination dataset.

# select the desired columns for further analysis for each DataFrame
vac_and_death_cols = ['location', 'date', 'total_vaccinations', 'people_vaccinated', 'people_fully_vaccinated', \
                      'new_vaccinations', 'new_vaccinations_smoothed','total_deaths', 'new_deaths'] 

happiness_cols = ['Country name', 'Regional indicator', 'Social support', 
                  'Healthy life expectancy', 'Freedom to make life choices', 'Generosity',
                 'Perceptions of corruption']
population_cols = ['Country (or dependency)', 'Population (2020)', 'Density (P/Km²)', 'Med. Age']

# keep the desired columns in the DataFrame.
vac_and_death = vac_and_death[vac_and_death_cols]
happiness = happiness[happiness_cols]
population = population[population_cols]

# merge the happiness and population by each country and name it df. 
df = happiness.merge(population, left_on='Country name', right_on='Country (or dependency)')

# for the vac_and_death dataset, we only keep the rows which the countries appear in df.
country_set = set(df['Country name'].values)
vac_and_death = vac_and_death[vac_and_death.location.isin(country_set)]

Since our research question is "How the onset of vaccination, the vaccination rates, and the death rate in a country are related to the happiness score of that country", we need to determine the onset dates for each country before doing further analysis.

As a result, we have decided to use the first date when each country has a non_na value of new_vaccinations_smoothed given the fact that this column has the least missing values. To make it happens, we have only selected the columns of date, location, and new_vaccinations_smoothed. We saved it to a temporary DataFrame and groupby it by the location. This is because we are interested in the onset date for each country.

After observing the dataset, we have found out that if the country has not had any person getting vaccinated, the csv file use NaN for the missing values. Thus, the first date with non-NaN value is the major vaccination date. We have applied a lambda function to drop all the NaN values and find the date that has the minimun value (the earliest date which is the onset date).

We have saved those dates into a dictionary where the key-value pairs are the countries and their corresponding onset date.

vac_and_death_temp = vac_and_death[['date', 'location', 'new_vaccinations_smoothed']]
onset_date = vac_and_death_temp.groupby('location')[['date', 'new_vaccinations_smoothed']]\
                            .apply(lambda df: df.dropna().date.min())
onset_date = onset_date.to_dict()

# dictionary with the key-value pairs of countries and their corresponding onset dates
# for cleaner view of this notebook, we have only displayed the first five country: date pairs
[f'{country}: {onset_date}' for country, onset_date in onset_date.items()][:5]

['Afghanistan: 2021-02-23',
 'Albania: 2021-01-11',
 'Algeria: 2021-01-30',
 'Argentina: 2020-12-30',
 'Armenia: 2021-04-01']

In order to calculate the mean of the vaccination rate cross {7, 15, 30, 60, 90, 180, and 360} days, we tried to find the onset date of the vaccinations in each country and calculate the average number of vaccinations injected since the onset date.

Therefore, we initially set the onset date in each country to the first date of new_vaccination(daily vaccination) data available.

However, we notice that there are exceptions. For instance, in Denmark, this country only had 2 vaccinations in the first approximately 15 days and had over 1000 daily vaccination in the next few days. We can see that the onset date of the vaccination is not the actual date the vaccinations were given to the public. Therefore, it is necessary to make a more inclusive definition for the onset date so that we can better deal with these exceptions.

As a result, we calculated the ratio of new_vaccinations increasing rate for each day. If the number of the new vaccinations has over 100 times of the one in the previous date, then we define this country as an exception which possibly has some anomaly in terms of new_vaccinations.

def check(ratio):
    #Make sure it has to be bounded by infinity
    if ratio > 100 and ratio < float('inf'):
        return True
    return False

#Apply the function to the values of new_vaccinations_smoothed on the neighbour rows to determine which two days has
#satisfy the conditions of 100 < ratio < infinity, where 100 is an arbitary number that signifies 
#a substantial increase.
if_ratio_greater_than_100 = (vac_and_death['new_vaccinations_smoothed'] 
                             / vac_and_death['new_vaccinations_smoothed'].shift(1)).apply(check)

vac_and_death['ratio_greater_than_100_p_v'] = if_ratio_greater_than_100
vac_and_death_true = vac_and_death[vac_and_death['ratio_greater_than_100_p_v'] == True]
vac_and_death_true

	location	date	total_vaccinations	people_vaccinated	...	new_vaccinations_smoothed	total_deaths	new_deaths	ratio_greater_than_100_p_v
31506	Denmark	2020-12-27	6017.0	6017.0	...	859.0	1174.0	21.0	True
45268	Ghana	2021-05-25	NaN	NaN	...	7801.0	783.0	0.0	True
59429	Jamaica	2021-06-05	NaN	NaN	...	336.0	964.0	4.0	True
113812	Switzerland	2020-12-23	429.0	405.0	...	214.0	7203.0	93.0	True
125326	Uruguay	2021-03-01	18406.0	18406.0	...	9017.0	611.0	3.0	True

5 rows × 10 columns

After taking closer look to the above countries in the original data table, we have found that Jamaica has a huge number of vaccination during its onset date because it only has few records. As a result, we see it as an outlier that could be discarded by our analysis. Thus, we had to remove Jamaica from our onset_date dictionary.

On the other hand, we have reset the onset date for those countries that showed a significant gap between two dates of new vaccinations (over 100 times of increasing). We reset the onset date to ensure that the onset date is the representation of when the vaccinations is carried out to the public.

# pop out the country of Jamaica
onset_date.pop('Jamaica', None)
# reset the onset date for Denmark, Switzerland, Uruguay
onset_date['Denmark'] = '2020-12-27'
onset_date['Switzerland'] = '2020-12-23'
onset_date['Uruguay'] = '2021-03-01'

# merge the DataFrame bulit of the onset_date dictioanry to the vac_and_death main DateFrame by location and index
vac_and_death = vac_and_death.merge(pd.Series(onset_date).to_frame().reset_index(), \
                                    left_on='location', right_on='index')

# we only want the date here, so we have converted them into a datetime object
vac_and_death.date = pd.to_datetime(vac_and_death.date)
vac_and_death[0] = pd.to_datetime(vac_and_death[0])

# after getting the onset date for each countries, we can subtract the date from its own onset date to 
# obtain a time delta since the onset date
vac_and_death = vac_and_death.dropna(subset=['new_vaccinations_smoothed'])
vac_and_death['since_onset_by_group'] = (vac_and_death.date - vac_and_death[0]).dt.days
vac_and_death.head()

	location	date	total_vaccinations	people_vaccinated	...	ratio_greater_than_100_p_v	index	0	since_onset_by_group
365	Afghanistan	2021-02-23	NaN	NaN	...	False	Afghanistan	2021-02-23	0
366	Afghanistan	2021-02-24	NaN	NaN	...	False	Afghanistan	2021-02-23	1
367	Afghanistan	2021-02-25	NaN	NaN	...	False	Afghanistan	2021-02-23	2
368	Afghanistan	2021-02-26	NaN	NaN	...	False	Afghanistan	2021-02-23	3
369	Afghanistan	2021-02-27	NaN	NaN	...	False	Afghanistan	2021-02-23	4

5 rows × 13 columns

To further explore the vaccination increase for each country, we implemented the following design such that our vaccination and death data is grouped by countries, and then for each country, the average of daily vaccinations and death rate for {7, 15, 30, 60, 90, 180, 360} days starting from the onset day of the vaccination rate is taken.

# create a new DataFrame
vac_death_agg = pd.DataFrame()

# add the country names into the DateFrame
vac_death_agg['location'] = vac_and_death[vac_and_death.since_onset_by_group \
    <= 7].groupby('location')['new_vaccinations_smoothed'].mean().index

# define a list of time intervals
time_intervals = [7, 15, 30, 60, 90, 180, 360]


# iterate through all of the time intervals and calculate the average of new vaccinations for each time interval
for time_interval in time_intervals:
    vac_death_agg[f'new_vac_{time_interval}_days_raw'] = \
    vac_and_death[vac_and_death.since_onset_by_group <= time_interval]\
    .groupby('location')['new_vaccinations_smoothed'].mean().values
    
    vac_death_agg[f'new_death_{time_interval}_days_raw'] = \
    vac_and_death[vac_and_death.since_onset_by_group <= time_interval]\
    .groupby('location')['new_deaths'].mean().values

# merge the vac_and_death_agg into the main df DataFrame so that we could do further analysis
df = df.merge(vac_death_agg, left_on='Country name', right_on='location')

# we normalized the vaccination number increased for each country by its population 
for time_interval in time_intervals:
    df[f'new_vac_{time_interval}_days'] = \
    df[f'new_vac_{time_interval}_days_raw']/df['Population (2020)']
    df = df.drop(columns=[f'new_vac_{time_interval}_days_raw'])
    
    df[f'new_death_{time_interval}_days'] = \
    df[f'new_death_{time_interval}_days_raw']/df['Population (2020)']
    df = df.drop(columns=[f'new_death_{time_interval}_days_raw'])

onset_df = pd.Series(onset_date).to_frame().reset_index()
onset_df.columns = ['index', 'onset_date']
df = df.merge(onset_df, left_on='Country name', right_on='index')
df = df.drop(['index'], axis=1)
df.head()

	Country name	Regional indicator	Social support	Healthy life expectancy	...	new_death_180_days	new_vac_360_days	new_death_360_days	onset_date
0	Finland	Western Europe	0.954	72.0	...	4.067209e-07	0.004752	3.649659e-07	2021-01-01
1	Denmark	Western Europe	0.954	72.7	...	1.412142e-06	0.004531	9.599740e-07	2020-12-27
2	Switzerland	Western Europe	0.942	74.4	...	2.380255e-06	0.004052	1.550371e-06	2020-12-23
3	Iceland	Western Europe	0.983	73.0	...	1.617216e-08	0.005384	4.736506e-08	2020-12-31
4	Netherlands	Western Europe	0.942	72.4	...	1.916123e-06	0.004669	1.321419e-06	2021-01-07

5 rows × 27 columns

Data Analysis & Results

EDA

*Note 1: Many Visualizations are animated to demonstrate change in pattern as a matter of various time intervals, and some can be interacted. For best visualization and interaction effects, it's strongly recommended to run the notebook in an ipython environment. Alternatively, you may find *.gif inside the visualization directory which are saved versions of the animated visualizations demonstrated in this notebook.

*Note 2: Jupyter Notebook doesn't work well with matplotlib on notebook mode. In particular, the notebook may compress some output visualization cells into scrollable format, which negatively impacts viewing experience. We've tried to programmatically change this behavior, but it still happens sometimes. When it occurs, select the cell. Then in the menu, click the following sequence: Cell -> Current Output -> Toggle Scrolling

Most countries that are available in the geopandas package are taken into account in our model. There are countries that are excluded from our model, indicated by the light blue color on the map, most of them are developing third-world countries in Africa.

The possible reasons might be the fact that these countries don’t have the resources to collect data or these data aren’t publically available or they just don’t have a sufficient population base. Because these countries are mostly developing ones, they might include a higher death rate and a lower vacciantion rate. In the scope of analysis, we need to keep in mind about the potantial biases and assumptions we made here. When proceeding with the analysis and the discussion, we’ll also make sure that our analysis doesn’t discriminate against those countries.

country_name_to_replace = {
    'United States': 'United States of America',
    'Bosnia and Herzegovina': 'Bosnia and Herz.',
    'Dominican Republic': 'Dominican Rep.',
    'North Macedonia': 'Macedonia',
}

# Countries that cannot be shown with geopandas world's map: 
# Bahrain, Malta, Singapore, Mauritius, Maldives, Comoros

new_country_lst = []
for c in df['Country name'].values:
    if c in country_name_to_replace:
        c = country_name_to_replace[c]
    new_country_lst.append(c)
df['Country name'] = new_country_lst

style.use('fivethirtyeight')
plt.rcParams['figure.figsize'] = [9.8, 6]
# Plot the countries we will analyze versus the countries we won't
world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))[['name', 'geometry']]
avail_countries = world.merge(df[['Country name']], left_on='name', right_on='Country name', how='left')
avail_countries['avail'] = ~avail_countries['Country name'].isna().values
avail_countries.avail = avail_countries.avail.replace({False: 'Not Analyzed', True: 'Analyzed'})
avail_countries.plot(column='avail', legend=True, categorical=True,);
plt.title('Countries in the Scope of Our Analysis');

*The above figure is static when the code cell is properly run.

By plotting the overall distributions of various happiness metrics for social support, healthy life expectancy, perception of corruption, and generosity, we could have a better idea of what the distributions look like by visualizing them. In our graph, we can observe a strong left-skewed distribution for both Social Support and Perceptions of Corruption, a left-skewed distribution for Healthy Life Expectancy, and a roughly normal distribution of generosity (center around 0). People in most countries are satisfied with their social support, a life expectancy above 65. But they tend to believe that their countries have a high degree of corruption and a neutral generosity.

plt.rcParams['figure.figsize'] = [9.8, 6]
plt.rcParams.update({'font.size': 10})

f, axes = plt.subplots(2, 2)
def plot_stationary_hist(ax, var, label, bins=20):
    sns.histplot(data=df, x=var, ax=ax, bins=bins)
    ax.set_xlabel(label)
# Plot the distribution of the four happiness metrics we will use
plot_stationary_hist(axes[0][0], 'Social support', 'Social Support')
plot_stationary_hist(axes[0][1], 'Healthy life expectancy', 'Healthy Life Expectancy')
plot_stationary_hist(axes[1][0], 'Perceptions of corruption','Perceptions of Corruption')
plot_stationary_hist(axes[1][1], 'Generosity','Generosity')
f.suptitle('Overall Distribution of Various Happiness Metrics');

*The above figure is static when the code cell is properly run.

In the below figure, the top-left graph displays the overall distribution in average new vaccination rates across different time spans (i.e. 7, 15, 30, 60, 180, 360 days). But the graphs seem to be strongly left-skewed and display an exponentially decreasing trend. Since most countries started from a small or zero vaccination population, we see that vaccination rates are clustered at a lower value from the first seven days. The top right graph is the visualization of the average new death rate across different time spans. We also observed a low death rate at the beginning and followed an increasing trend in the death rate over the next several time spans. To make the distribution more symmetric, we take the logarithm of both the average new vaccination rate and death rate. We can clearly see that both the average new vaccination rate and death rate have been transformed to rough normal distributions.

Thus, we are able to perceive the change of new vaccination rate and death rate more clearly. By observing the distribution change across different time spans (i.e. 7, 15, 30, 60, 180, 360 days), we can see that the average new vaccination rate and average new death rate gradually shift from left to right. The logarithm of the new vaccination rate lost its symmetry and became right-skewed where it gradually shifted to higher vaccination rates since the majority of the countries have started to implement vaccination on a large scale. The new death rate logarithm model clearly displayed an increase in death rate as it also became right-skewed. Despite the increasing vaccination rate across the time, the potential reason for the increasing death rate is because of the widespread and transmission speed of the disease.

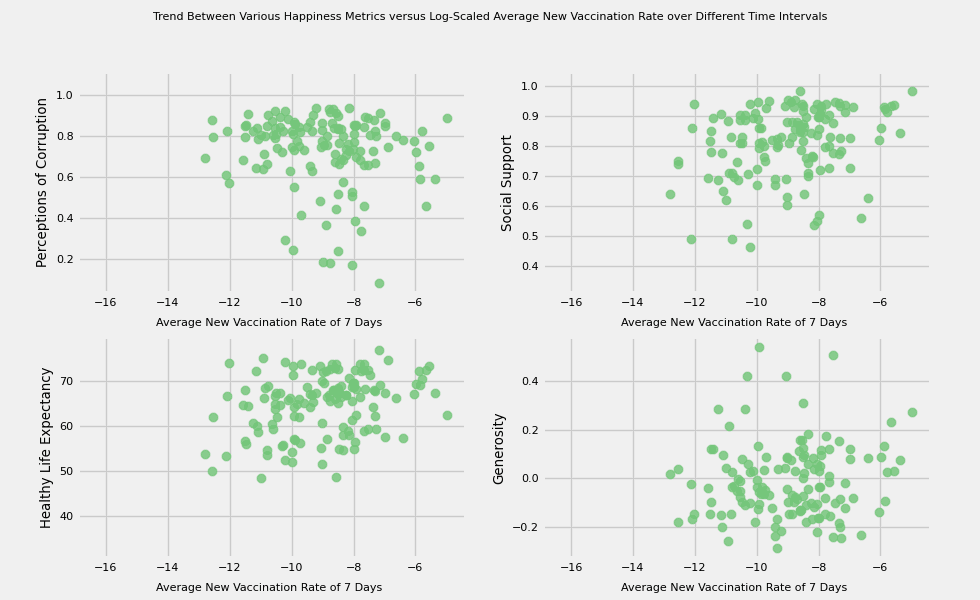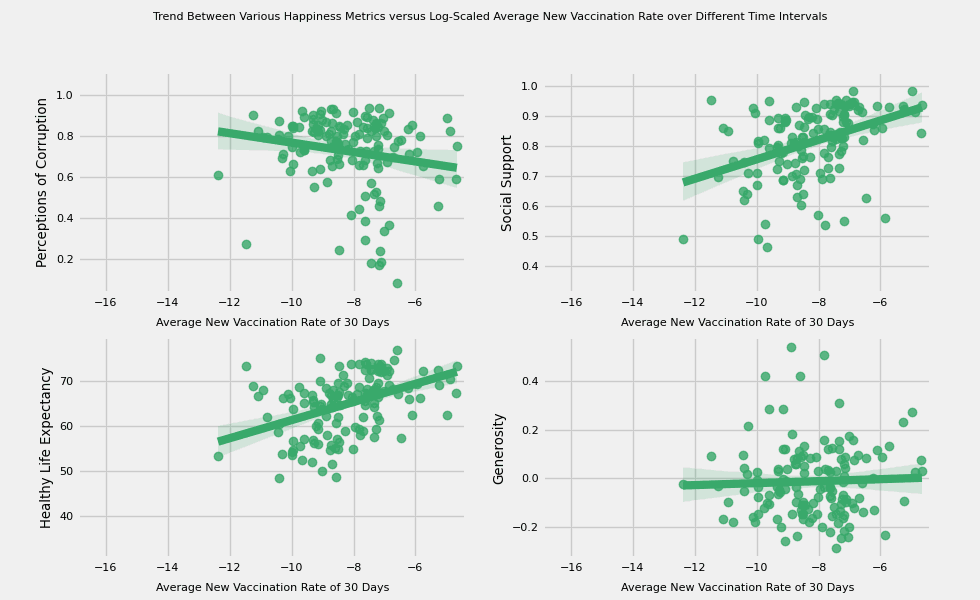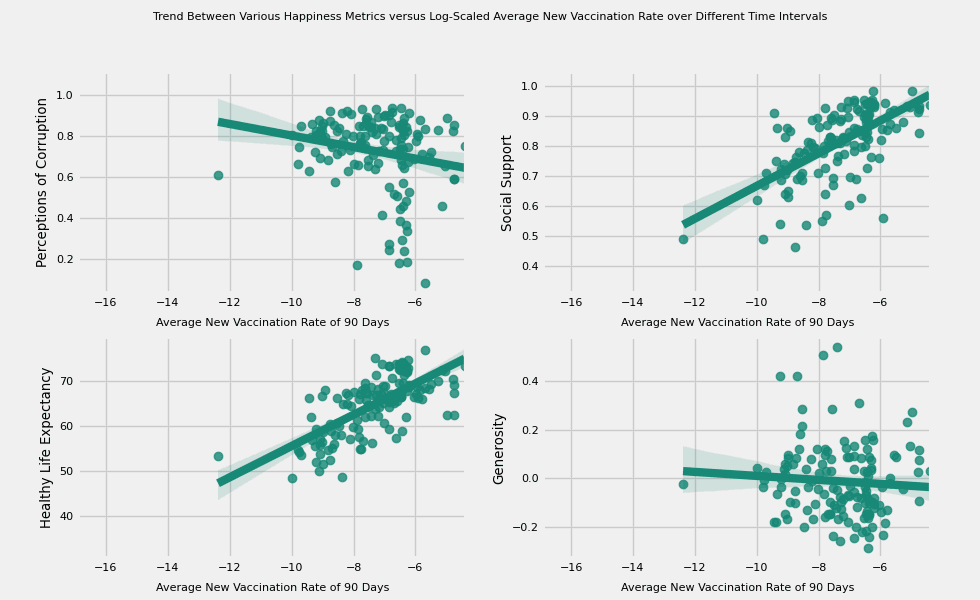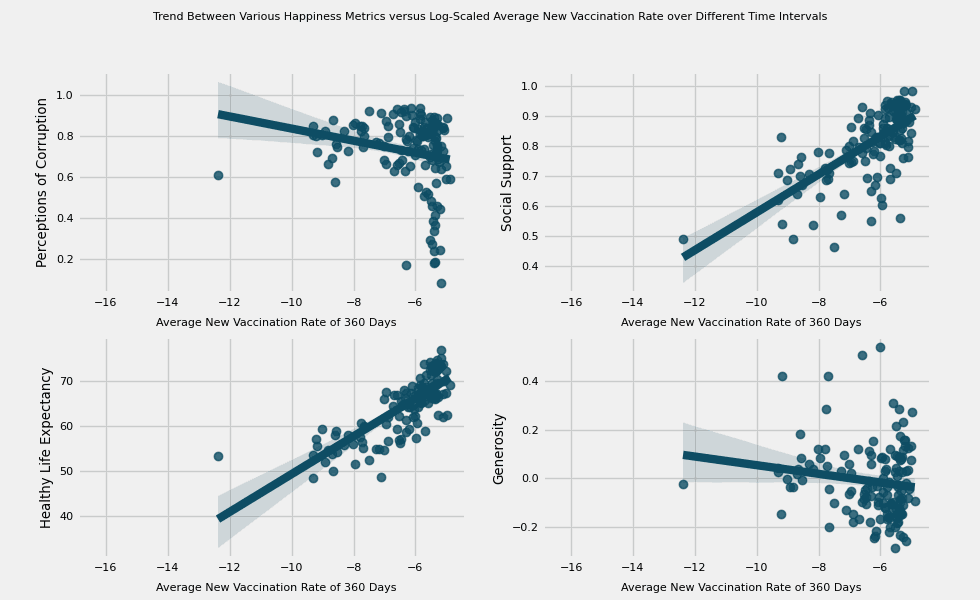
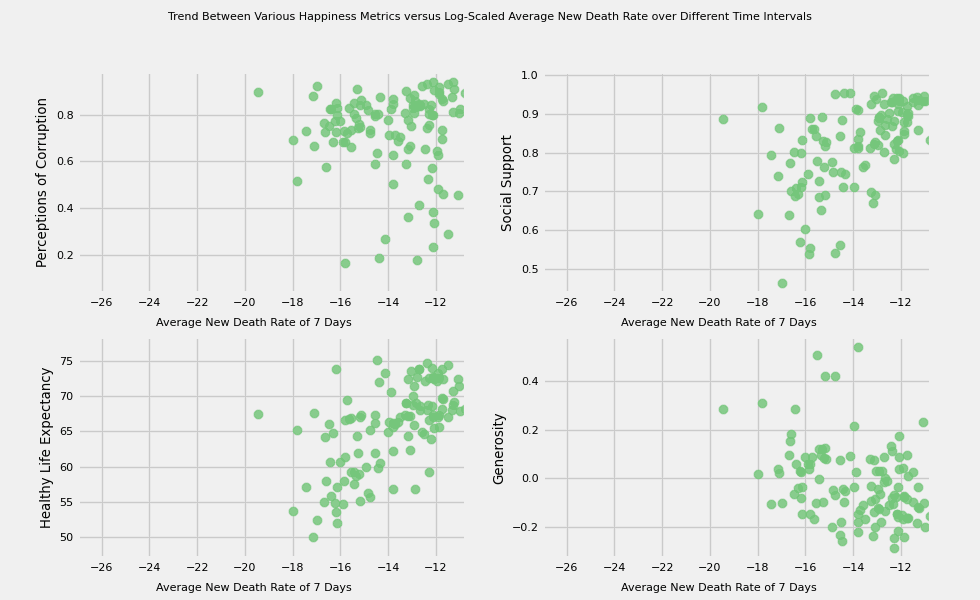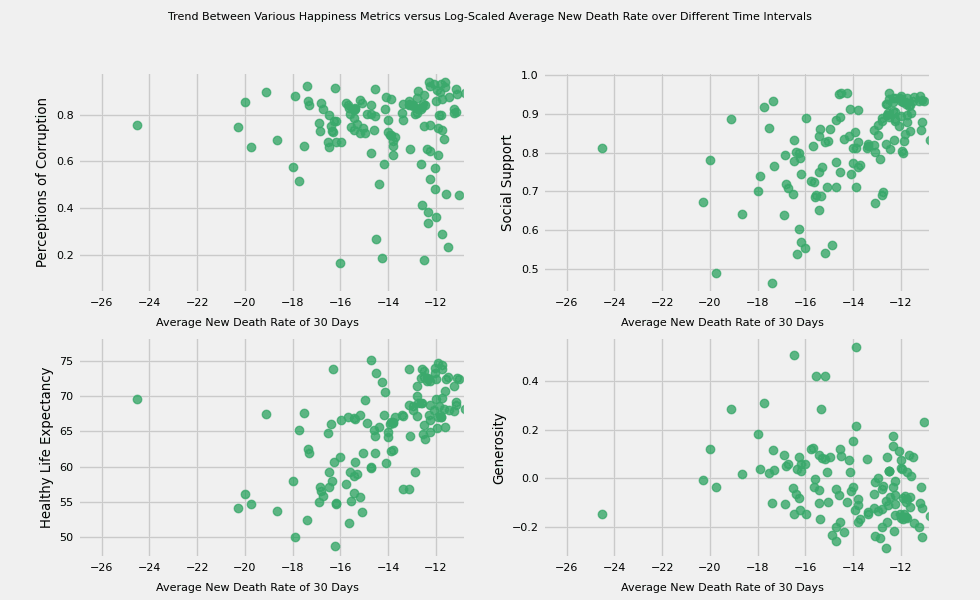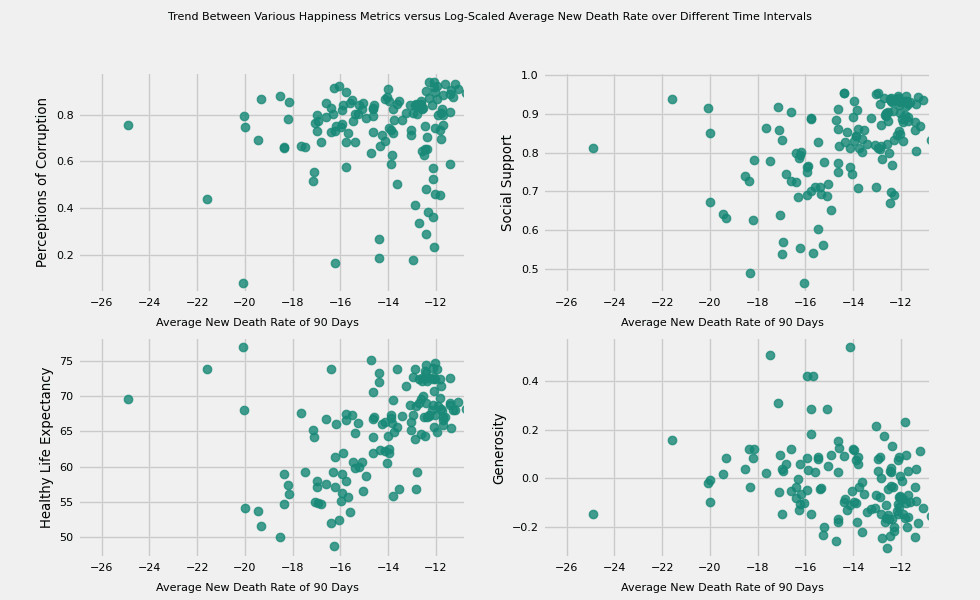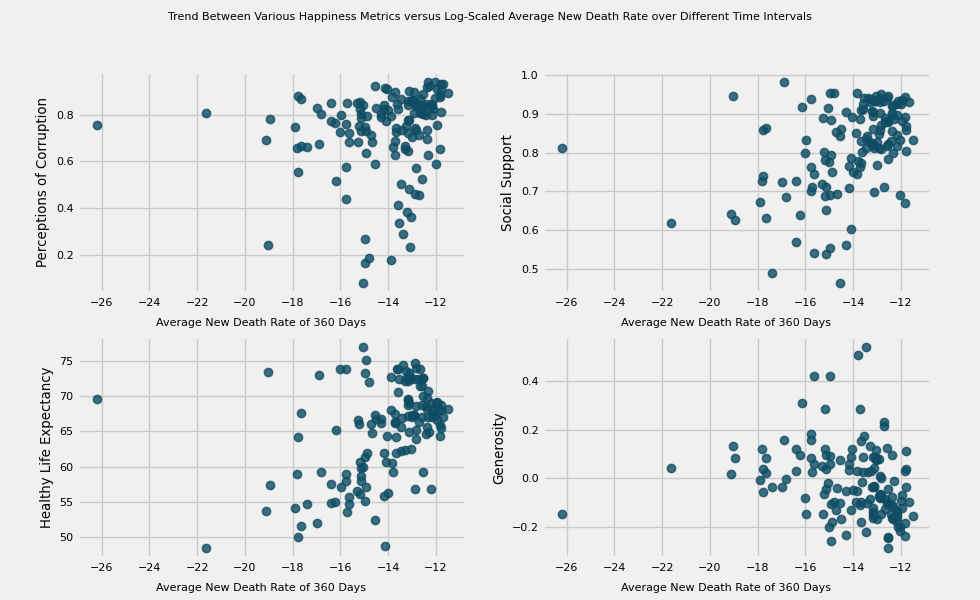
# https://hihayk.github.io/scale/#4/6/50/80/-51/67/20/14/1D9A6C/29/154/108/white
colors = [
    '#0A2F51',
    '#0E4D64',
    '#137177',
    '#188977',
    '#1D9A6C',
    '#39A96B',
    '#56B870',
    '#74C67A',
]
colors.reverse()
plt.rcParams['figure.figsize'] = [9.8, 6]
plt.rcParams.update({'font.size': 8})

# to visualize -inf at log scale
eps = 1e-5

f, axes = plt.subplots(2, 2)
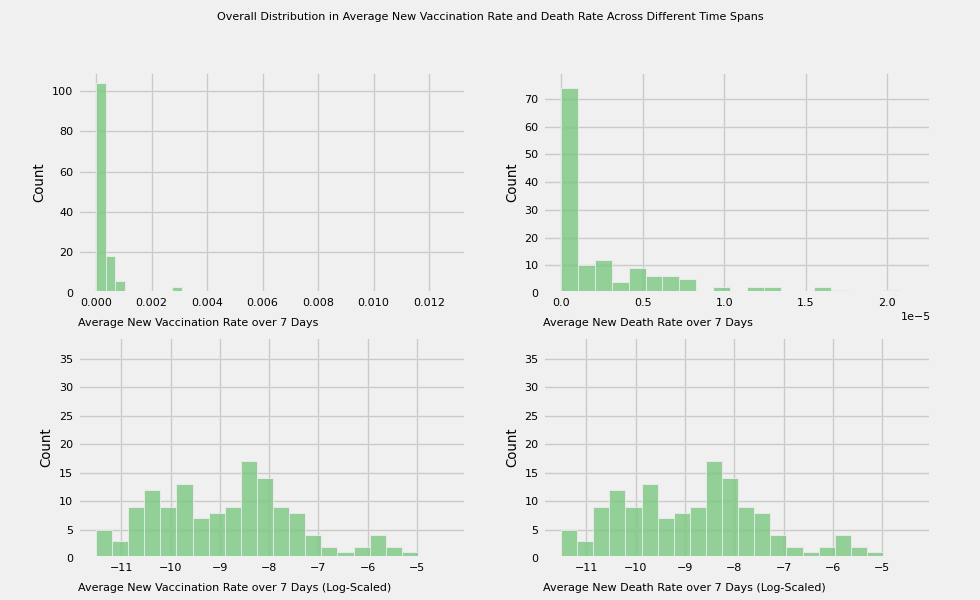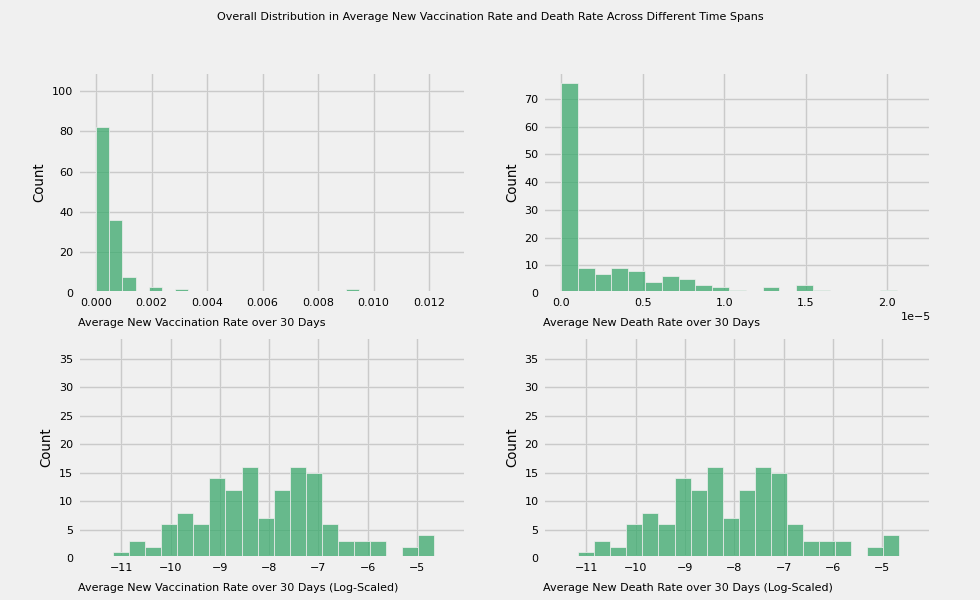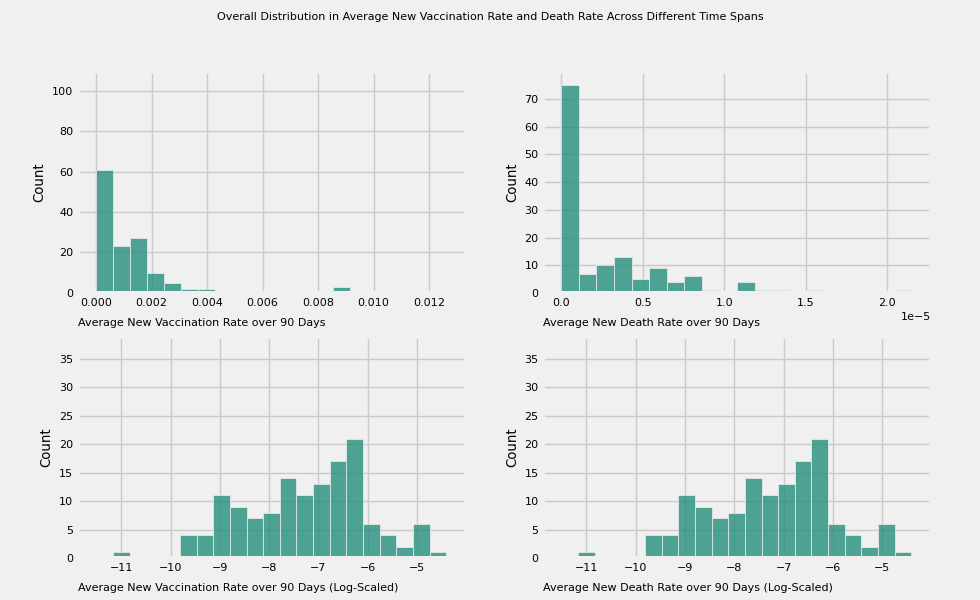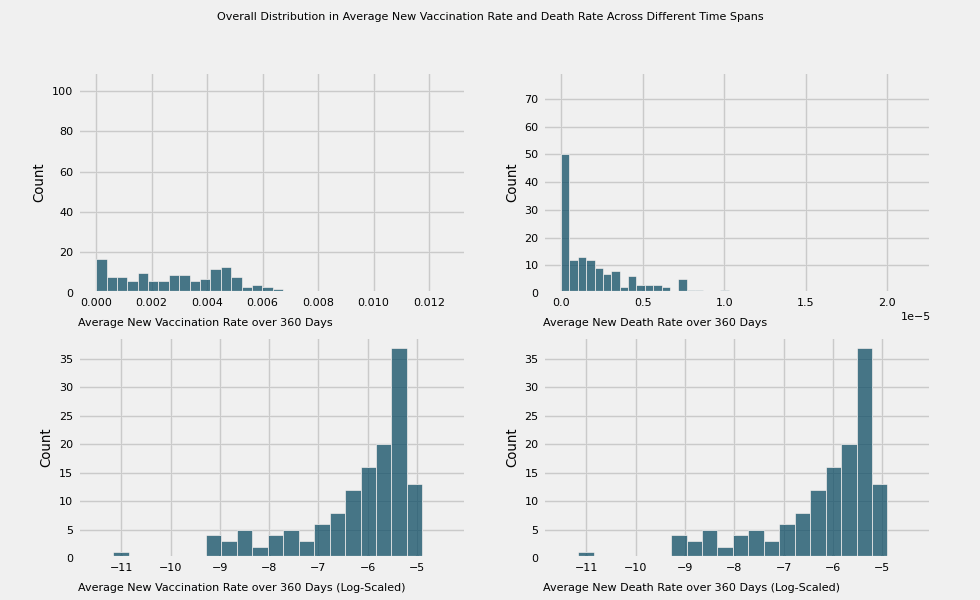
title = 'Overall Distribution in Average New Vaccination Rate and Death Rate Across Different Time Spans'
f.suptitle(title, 
           size='medium')
camera = Camera(f)
def plot_animation_hist(ax, var=None, label=None, color=None, bins=20, manual_entry=False, data=None):
    if not manual_entry:
        sns.histplot(x=var, data=df, ax=ax, color=color, bins=bins)
    else:
        sns.histplot(x=data, ax=ax, color=color, bins=bins)
    ax.text(0, -0.15, label, transform=ax.transAxes)
    ax.set_xlabel('')
# Plot the average new vaccination rate and death across different time spans:
# 7, 15, 30, 60, 180, 360 days
vac_to_plot = [f'new_vac_{number}_days' for number in time_intervals]
death_to_plot = [f'new_death_{number}_days' for number in time_intervals]
for i in range(len(vac_to_plot)):
    plot_animation_hist(axes[0][0], vac_to_plot[i], color=colors[i],
                        label=f'Average New Vaccination Rate over {time_intervals[i]} Days')
    plot_animation_hist(axes[0][1], death_to_plot[i], color=colors[i],
                        label=f'Average New Death Rate over {time_intervals[i]} Days')
    plot_animation_hist(axes[1][0], color=colors[i], manual_entry=True, data=np.log(df[vac_to_plot[i]] + eps),
                        label=f'Average New Vaccination Rate over {time_intervals[i]} Days (Log-Scaled)')
    plot_animation_hist(axes[1][1], color=colors[i], manual_entry=True, data=np.log(df[vac_to_plot[i]] + eps),
                        label=f'Average New Death Rate over {time_intervals[i]} Days (Log-Scaled)')
    camera.snap()
animation = camera.animate(interval = 1500, repeat = True, repeat_delay = 0)
if not os.path.exists('visualizations'): os.makedirs('visualizations')
animation.save(f'visualizations/{title}.gif')
animation;

MovieWriter ffmpeg unavailable; using Pillow instead.

*The above figure is animated when the code cell is properly run.

In the below figure, we want to see the trend of the onset data of vaccination of each country with their corresponding happiness score metrics. Since we have considered 4 types of metrics for happiness score, there will be 4 corresponding scatter plots with least-squared regression lines with respect to each type of metric. If we look closer at each graph, we observe a slight positive slope between the perception of corruption and the number of days since the earliest onset & generosity and the number of days since the earliest onset, a moderate negative slope between social support and the number of days since the earliest onset & between health-life expectancy and the number of days since the earliest onset. This roughly shows that the earlier the countries get vaccinated, the higher the happiness score they have. This is true across all four types of happiness score measurement metrics.

Moreover, we have a corresponding scatter plot for each scatter plot that has a least-squared regression line. In each of those scatter plots, we have used different colors to represent the geography of each country so that we could have a better sense of the order of onset date for each cluster of countries. In the plots, we can see that the countries from Europe, North America, and East Asia are the countries that have earlier onset data of COVID-19 vaccination. This makes sense because the United States (from North America), the United Kingdom (Europe), and China (East Asia) are the earliest countries that have started to develop vaccines. We can also see that the developed countries from Europe, who are also the earliest countries that have started to get vaccinated have low scores of sense of corruption. As a result, we can use our previous knowledge to intuitively match our data and verify our conclusion makes sense.

plt.rcParams['figure.figsize'] = [9.8, 10]
plt.rcParams.update({'font.size': 7})
# Extract the columns that we want to analyze
onset_happiness = df[['Country name', 'Regional indicator', 'Perceptions of corruption',
                      'Social support', 'Healthy life expectancy', 'Generosity', 'onset_date']]
# Calculate after how many days people from a country gets vaccinated since
# the vaccination date of a country with the earliest vaccination onset date
onset_happiness['days_since_earlist'] = (pd.to_datetime(df['onset_date']) \
                                       - pd.to_datetime(df['onset_date']).min()).dt.days
# Make two seperate sets of scatter plots. Both of them are metrics for happiness versus 
# the number of days since the earlist onset for all countries. While plots in the first
# have a linear regression line, plots in the second set are hued by different regions
f, axes = plt.subplots(4, 2)
f.suptitle('Relationship Between Promptitude of Vaccination Onset versus Various Happiness Score Metrics', 
           size='medium')
columns_to_plot = ['Perceptions of corruption', 'Social support', 'Healthy life expectancy', 'Generosity']
for i in range(len(axes)):
    sns.regplot(x='days_since_earlist', y=columns_to_plot[i], 
                data=onset_happiness, ax=axes[i][0])
    axes[i][0].set_xlabel('Number of Days since the Earlist Onset among all Countries')
    axes[i][0].set_ylabel(columns_to_plot[i].title())
    sns.scatterplot(x='days_since_earlist', y=columns_to_plot[i], 
                    data=onset_happiness, hue='Regional indicator', ax=axes[i][1])
    axes[i][1].set_xlabel('Number of Days since the Earlist Onset among all Countries')
    axes[i][1].set_ylabel(columns_to_plot[i].title())
    axes[0][1].legend(bbox_to_anchor=(1, 1), loc='lower right', ncol=2)
    if i!= 0: axes[i][1].get_legend().remove()

*The above figure is static when the code cell is properly run.

def trend_animation(kw, label, title=None):
    def configure_subplot(ax, x, y):
        ax.text(0.2, -0.15, x, transform=ax.transAxes)
        ax.set_xlabel('')
        ax.set_ylabel(y)

    plt.rcParams['figure.figsize'] = [9.8, 6]
    plt.rcParams.update({'font.size': 8})
    # set the timespans for plots
    iterations_to_plot = [f'new_{kw}_{number}_days' for number in time_intervals]
    # Extract the happiness metrics that we want to analyze
    columns_to_plot = ['Perceptions of corruption', 'Social support', 'Healthy life expectancy', 'Generosity']

    vac_happiness = df[iterations_to_plot + columns_to_plot]
    for num_days in iterations_to_plot:
        vac_happiness[num_days] = np.log(vac_happiness[num_days])
    # Plot all four metrics versus the seclected column across all timespans
    f, axes = plt.subplots(2, 2)
    if title is not None: f.suptitle(title, size='medium')
    camera = Camera(f)
    for i in range(len(iterations_to_plot)):
        sns.regplot(x=iterations_to_plot[i], y=columns_to_plot[0], 
                            data=vac_happiness, ax=axes[0][0], color=colors[i])
        configure_subplot(axes[0][0], 
                          f'Average New {label} Rate of {time_intervals[i]} Days', 
                          'Perceptions of Corruption')
        sns.regplot(x=iterations_to_plot[i], y=columns_to_plot[1], 
                            data=vac_happiness, ax=axes[0][1], color=colors[i])
        configure_subplot(axes[0][1], 
                          f'Average New {label} Rate of {time_intervals[i]} Days', 
                          'Social Support')
        sns.regplot(x=iterations_to_plot[i], y=columns_to_plot[2], 
                            data=vac_happiness, ax=axes[1][0], color=colors[i])
        configure_subplot(axes[1][0], 
                          f'Average New {label} Rate of {time_intervals[i]} Days', 
                          'Healthy Life Expectancy')
        sns.regplot(x=iterations_to_plot[i], y=columns_to_plot[3], 
                            data=vac_happiness, ax=axes[1][1], color=colors[i])
        configure_subplot(axes[1][1], 
                          f'Average New {label} Rate of {time_intervals[i]} Days', 
                          'Generosity')
        camera.snap()
    animation = camera.animate(interval = 1500, repeat = True,
                               repeat_delay = 0)
    if not os.path.exists('visualizations'): os.makedirs('visualizations')
    animation.save(f'visualizations/{title}.gif')
    return animation

We want to further investigate the correlation between happiness metrics on perceptions of corruption, social support, healthy life expectancy, and generosity, and average new vaccination rate over time. However, there is no clear linear pattern between all the four happiness metrics and the average new vaccination rate in the 7-day time span. We gradually observe a linear pattern between all the four happiness metrics and the average new vaccination rate in the following time span measurements. Similar to the linear pattern in the graph above, we observe a positive slope between the perception of corruption and the number of days since the earliest onset & generosity and the number of days since the earliest onset, a negative slope between social support and the number of days since the earliest onset & between health-life expectancy and the number of days since the earliest onset. Both the positive and negative correlations get stronger as the time span for the average new vaccination rate measurement increases. This somehow intuitively makes sense. As the time span increases, our new vaccination rate data can better represent a country’s vaccination condition in the long term. (There could be a huge new vaccination in the first few days for countries with a small vaccination population. This sharp increase will be normalized if we have a longer time span). Thus, the relationship will be more clear.

# Plot all four metrics versus log-scaled new vaccination rate across all timespans
trend_animation('vac', 'Vaccination', 
    'Trend Between Various Happiness Metrics versus Log-Scaled Average New Vaccination Rate over Different Time Intervals')

MovieWriter ffmpeg unavailable; using Pillow instead.

<matplotlib.animation.ArtistAnimation at 0x7fbe40a523d0>

*The above figure is animated when the code cell is properly run.

We want to next investigate the correlation between happiness metrics on perceptions of corruption, social support, healthy life expectancy, and generosity, and average new death overtime. However, there is no clear linear pattern between all the four happiness metrics and the average new vaccination rate across all time spans (7, 15, 30, 60, 180, 360 days). Although we can’t draw a clear regression line in all distributions across the time spans, it is still possible to observe a slight linear trend. We observe a slight positive slope between the perception of corruption and the average new death rate, social support, and the average new death rate, & health life expectancy, and the average new death rate. We also observe a slight negative slope between the generosity and the new death rate. We discover that the death rate is associated with high healthy life expectancy and social support. This is because the disease was most widespread in countries in North America and Western Europe in the early days of the covid-19, the places with relatively high healthy life expectancy and social support scores. Therefore the massive death rate in North America and Western Europe caused by Covid-19 brings the overall death rate with high healthy life expectancy and social support scores.

# Plot all four metrics versus log-scaled new death rate across all time spans
trend_animation('death', 'Death', 
    'Trend Between Various Happiness Metrics versus Log-Scaled Average New Death Rate over Different Time Intervals')

MovieWriter ffmpeg unavailable; using Pillow instead.

<matplotlib.animation.ArtistAnimation at 0x7fbe305163a0>

*The above figure is animated when the code cell is properly run.

The below graph displays the relationship between the average new vaccination rate and death rate at different time intervals. It is clear that the new vaccination rate has been increasing across the time intervals since the countries started to gradually implement vaccination on a larger scale across the time intervals. Although the vaccination rate shows an increasing trend, the death rate experiences no visible changes.

# Make a dataframe with all the stats we want to plot across different time spans
def make_vd_stats(df, time_intervals, column_kw, category_name, melt=True, 
                  include_region=False, region_kw='Country name'):
    columns = [region_kw] if include_region else []
    columns += [f'new_{column_kw}_{number}_days' for number in time_intervals]
    data = df[columns]
    renamed_columns = [f'{number} Days since Onset' for number in time_intervals]
    data.columns = ['Region'] + renamed_columns if include_region else renamed_columns
    if melt:
        data = data.melt()
        data['Type'] = category_name
    return data

vac_data = make_vd_stats(df, time_intervals, 'vac', 'Vaccination Rate')
death_data = make_vd_stats(df, time_intervals, 'death', 'Death Rate')
# Concatenate our vaccination data with death rate data and take the logorithm of
# new death rate and new vaccination rate
vac_death_data = pd.concat([vac_data, death_data])
vac_death_data['Log-Scaled Rate'] = np.log(vac_death_data['value'])
# Make two set of boxplots on the distribution of the log-scaled new death rate and 
# new vaccination rate across the indicated time intervals
f, ax = plt.subplots()
sns.boxplot(data=vac_death_data, x="variable", y="Log-Scaled Rate", ax=ax, hue='Type')
ax.set_title('Relationship Between Average New Vaccination Rate and Death Rate at Different Time Intervals')
f.show();

*The above figure contains interaction when the code cell is properly run.

Finally, if we break down the death rate by regional indicator, and use number of days since the onset of vaccination, we found a thoughtful results, regions with mostly developed countries show a decreasing trend - that is, the longer the vaccination went, the lower the average new death rate was; on the other hand, regions with mostly developing countries show show an increasing trend in average new death rate. The reasons for the trend are unknown given the data we have, and possible explanations of this trend are discussed in later part of the project. This diverging results explain the reason why death overall (i.e. globally) as we moved forward from 7 days since onset all the way to 360 days since onset (data from different regions balance out each other).

# Make a dataframe with new death rates across all time spans and group by regions
death_data = make_vd_stats(df, time_intervals, 'death', 'Death Rate', melt=False, 
                           include_region=True, region_kw='Regional indicator')
death_data = death_data.melt(id_vars = ['Region'])
death_data['variable'] = death_data['variable'].apply(lambda s: int(s.split()[0]))
death_data.columns = ['Region', 'Number of Days Since Onset', 'Death Rate']
death_data = death_data.groupby(['Region', 'Number of Days Since Onset']).mean().reset_index()

source = death_data
selection = alt.selection_multi(fields=["Region"], bind="legend")
# Plot the trend of new death rates versus time spans by each region
alt.Chart(source).mark_line().encode(
    x = alt.X('Number of Days Since Onset', scale=alt.Scale(domain=[7, 360])),
    y='Death Rate',
    color='Region',
    opacity=alt.condition(selection, alt.value(1), alt.value(0.1))
).properties(
   height=300, width=650, 
    title='Trend in Average New Death Rate Across Different Regions Since the Day of Vaccination Onset'
).add_selection(
   selection
)

# press legend to select lines, press shift to select multiple lines

*The above figure contains interaction when the code cell is properly run.

Statistical Modeling

Now, after we visually analyzed relationships between our desired variables, we wanted to statistically establish some conclusions. Since we observed a similar scatter plot trend between all happiness metrics v.s. different time spans, we decided to perform a Principal Component Analysis (PCA) on average new vaccination and death rate to achieve dimension reduction (and thus attempting to exclude the effect of multicollinarity on our model). According to the cumulative explained variance plot below, it shows that around 95 percent of the variance can be explained by one component of the New Average Death Rate and two components of the New Average Vaccination Rate. Thus, we can reduce the dimension of 7 for the New Average Death Rate to 1 and reduce the dimension of 7 for the Average New Vaccination Rate to 2.

# an arbitarally small constant that prevents some data causing weird output after applying log,
# given log(0) = DNE
eps=1e-7
# we selected our features to be the new vaccination rates and the new death rates for 7, 15, 30, 60,
# 90, 180, and 360 days.
features = df[['new_vac_7_days', 'new_death_7_days', 'new_vac_15_days',
       'new_death_15_days', 'new_vac_30_days', 'new_death_30_days',
       'new_vac_60_days', 'new_death_60_days', 'new_vac_90_days',
       'new_death_90_days', 'new_vac_180_days', 'new_death_180_days',
       'new_vac_360_days', 'new_death_360_days']]
# impute the missing values since PCA cannot handle missing values
features = features.fillna(features.mean())
# normalize the distribution
features = np.log(features + eps)
# promptitude, which is the days since the earliest onset date for vaccination in each country
features['promptitude'] = (pd.to_datetime(df.onset_date) - \
                           pd.to_datetime(df.onset_date).min()).dt.days
# extract and process the testing features
outcomes_cols = ['Social support', 'Healthy life expectancy', \
                 'Perceptions of corruption', 'Generosity']

predictor_str = ' + '.join(features.columns)

complete_df = pd.concat([features, df[outcomes_cols]], axis=1)
complete_df.columns = complete_df.columns.str.replace(' ','_')

vac_cols = [f'new_vac_{time}_days' for time in time_intervals]
death_cols = [f'new_death_{time}_days' for time in time_intervals]

# set fratures of the visulization
plt.rcParams['figure.figsize'] = [9.8, 5]
f, ax = plt.subplots()

# use a PCA to compress the dimensions of the model given the distribution is similar
# PCA plot of New Average Vaccination Rate
pca = PCA().fit(complete_df[vac_cols])
ax.plot([0] + list(np.cumsum(pca.explained_variance_ratio_)), label='New Average Vaccination Rate')
# PCA plot of New Average Death Rate
pca = PCA().fit(complete_df[death_cols])
ax.plot([0] + list(np.cumsum(pca.explained_variance_ratio_)), label='New Average Death Rate')
ax.set_xlabel('Number of Components')
ax.set_ylabel('Cumulative Explained Variance')

ax.legend()

f.suptitle('Cumulative Explained Variance on Average New Vaccination/Death Rate via PCA');
f.show()

By implementing the dimension reduced to our DataFrame, we are now able to use only four features:

• VRD1 (Vaccination Rate, Dimension 1)
• VRD2 (Vaccination Rate, Dimension 2)
• DRD1 (Death Rate, Dimension 1)
• PROMPTITUDE (The difference in days between a country that started vaccination and the country that started vaccination the earliest among countries we take into account)

We will then analyze their correlation to the happiness metrics and proceed to the modeling steps. For modeling, we used $\alpha = 0.01$ for significance.

# set new dimension for new average vaccination rate
VRD_NUM = 2
vaccination_rate_features = PCA(VRD_NUM).fit_transform(complete_df[vac_cols])

# set new dimension for new average death rate
DRD_NUM = 1
death_rate_features = PCA(DRD_NUM).fit_transform(complete_df[death_cols])
# select the predictor columns
predictor_cols = [f'VRD{i}' for i in range(1, VRD_NUM+1)] + \
                [f'DRD{i}' for i in range(1, DRD_NUM+1)] + \
                ['PROMPTITUDE']
# select the outcome columns
outcomes_cols = ['Social_support', 'Healthy_life_expectancy', \
                 'Perceptions_of_corruption', 'Generosity']
# generate a new DataFrame with newest features
features = pd.DataFrame(np.concatenate([vaccination_rate_features, 
                             death_rate_features,
                             features[['promptitude']].values,
                             complete_df[outcomes_cols].values], axis=1),
                        columns=predictor_cols+outcomes_cols)
predictor_str = ' + '.join(predictor_cols)
features.head(5)

	VRD1	VRD2	DRD1	PROMPTITUDE	Social_support	Healthy_life_expectancy	Perceptions_of_corruption	Generosity
0	-1.998782	1.066470	-1.170656	29.0	0.954	72.0	0.186	-0.098
1	-1.892923	0.697582	2.399335	24.0	0.954	72.7	0.179	0.030
2	-0.564930	1.997444	4.358298	20.0	0.942	74.4	0.292	0.025
3	-2.195527	1.309696	-5.885623	28.0	0.983	73.0	0.673	0.160
4	-2.935554	0.453669	3.319475	35.0	0.942	72.4	0.338	0.175

We build an OLS regression model to find the correlation between the independent variables: VRD1, VRD2, DRD1, and PROMPTITUDE with the dependent variable: Social Support. We see that the R-squared score is moderately high with $$R^2 = 0.545$$ This means that 54.5% of the variation of Social Support could be explained by these independent variables.

In the summary, we can see that the p-values for VRD1, VRD2, and DRD1 are all statistically significant given they are all less than $$\alpha = 0.01$$ However, the PROMPTITUDE displays less statistical significance with a p-value of 0.258 when the significance level is low. This is possibly due to the fact that all other factors are explained well.

# build an OLS model of the four features and social support
outcome, predictors = patsy.dmatrices(
    f"{outcomes_cols[0].replace(' ', '_')} ~ {predictor_str}", features)
model = sm.OLS(outcome, predictors)
# print out the summary of the OLS model
results = model.fit()
results.summary()

OLS Regression Results

Dep. Variable:	Social_support	R-squared:	0.549
Model:	OLS	Adj. R-squared:	0.535
Method:	Least Squares	F-statistic:	40.75
Date:	Wed, 08 Dec 2021	Prob (F-statistic):	2.61e-22
Time:	20:29:06	Log-Likelihood:	157.85
No. Observations:	139	AIC:	-305.7
Df Residuals:	134	BIC:	-291.0
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	0.8328	0.017	49.556	0.000	0.800	0.866
VRD1	-0.0123	0.003	-4.819	0.000	-0.017	-0.007
VRD2	0.0282	0.006	5.122	0.000	0.017	0.039
DRD1	0.0055	0.002	2.682	0.008	0.001	0.010
PROMPTITUDE	-0.0002	0.000	-1.138	0.257	-0.001	0.000

Omnibus:	24.159	Durbin-Watson:	1.684
Prob(Omnibus):	0.000	Jarque-Bera (JB):	33.157
Skew:	-0.946	Prob(JB):	6.31e-08
Kurtosis:	4.465	Cond. No.	224.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

We build an OLS regression model to find the correlation between the independent variables: VRD1, VRD2, DRD1, and PROMPTITUDE with the dependent variable: Healthy_life_expectancy. We see that the R-squared score is the highest among all the OLS models with $$R^2 = 0.677$$ This means that 67.7% of the variation of Healthy_life_expectancy could be explained by these independent variables.

In the summary, we can see that the p-values for VRD1, VRD2, and DRD1 are all statistically significant given they are all less than $$\alpha = 0.01$$ However, the PROMPTITUDE displays less statistical significance with a p-value of 0.088 when the significance level is low.

# build an OLS model of the four features and Healthy_life_expectancy
outcome, predictors = patsy.dmatrices(
    f"{outcomes_cols[1].replace(' ', '_')} ~ {predictor_str}", features)
model = sm.OLS(outcome, predictors)
# print out the summary of the OLS model
results = model.fit()
results.summary()

OLS Regression Results

Dep. Variable:	Healthy_life_expectancy	R-squared:	0.682
Model:	OLS	Adj. R-squared:	0.673
Method:	Least Squares	F-statistic:	71.97
Date:	Wed, 08 Dec 2021	Prob (F-statistic):	1.98e-32
Time:	20:29:06	Log-Likelihood:	-379.31
No. Observations:	139	AIC:	768.6
Df Residuals:	134	BIC:	783.3
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	66.3090	0.801	82.762	0.000	64.724	67.894
VRD1	-0.8273	0.121	-6.815	0.000	-1.067	-0.587
VRD2	1.8179	0.263	6.923	0.000	1.299	2.337
DRD1	0.2651	0.098	2.692	0.008	0.070	0.460
PROMPTITUDE	-0.0176	0.010	-1.733	0.085	-0.038	0.002

Omnibus:	2.502	Durbin-Watson:	1.519
Prob(Omnibus):	0.286	Jarque-Bera (JB):	2.406
Skew:	0.026	Prob(JB):	0.300
Kurtosis:	3.642	Cond. No.	224.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

We build an OLS regression model to find the correlation between the independent variables: VRD1, VRD2, DRD1, and PROMPTITUDE with the dependent variable: Perceptions_of_corruption. We see that the R-squared score is the lowest with $$R^2 = 0.114$$. This means that only 11.4% of the variation of Perceptions_of_corruption could be explained by these independent variables.

In the summary, we can see that the p-values for VRD1, VRD2, and PROMPTITUDE are all NOT statistically significant given they are all greater than $$\alpha = 0.01$$ However, the DRD1 displays statistical significance with a p-value of 0.003.

# build an OLS model of the four features and Perceptions_of_corruption
outcome, predictors = patsy.dmatrices(
    f"{outcomes_cols[2].replace(' ', '_')} ~ {predictor_str}", features)
model = sm.OLS(outcome, predictors)
# print out the summary of the OLS model
results = model.fit()
results.summary()

OLS Regression Results

Dep. Variable:	Perceptions_of_corruption	R-squared:	0.117
Model:	OLS	Adj. R-squared:	0.090
Method:	Least Squares	F-statistic:	4.432
Date:	Wed, 08 Dec 2021	Prob (F-statistic):	0.00214
Time:	20:29:06	Log-Likelihood:	49.139
No. Observations:	139	AIC:	-88.28
Df Residuals:	134	BIC:	-73.60
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	0.7208	0.037	19.622	0.000	0.648	0.793
VRD1	0.0147	0.006	2.643	0.009	0.004	0.026
VRD2	-0.0284	0.012	-2.362	0.020	-0.052	-0.005
DRD1	0.0137	0.005	3.028	0.003	0.005	0.023
PROMPTITUDE	7.031e-05	0.000	0.151	0.880	-0.001	0.001

Omnibus:	37.844	Durbin-Watson:	1.247
Prob(Omnibus):	0.000	Jarque-Bera (JB):	58.867
Skew:	-1.399	Prob(JB):	1.65e-13
Kurtosis:	4.526	Cond. No.	224.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

We build an OLS regression model to find the correlation between the independent variables: VRD1, VRD2, DRD1, and PROMPTITUDE with the dependent variable: Generosity. We see that the R-squared score is similar to the R-Squared score above with $$R^2 = 0.124$$ which corresponds to a weak correlation that only 12.4% of the variation of Generosity could be explained by these independent variables.

In the summary, we can see that only DRD1 is statistically significant given the fact that the p-values for the rest of the independent variables are all greater than $$ \alpha = 0.01$$ Thus, we can conclude that there isn’t a correlation between VRD1, VRD2, and PROMPTITUDE and Generosity.

# build an OLS model of the four features and Generosity
outcome, predictors = patsy.dmatrices(
    f"{outcomes_cols[3].replace(' ', '_')} ~ {predictor_str}", features)
model = sm.OLS(outcome, predictors)
# print out the summary of the OLS model
results = model.fit()
results.summary()

OLS Regression Results

Dep. Variable:	Generosity	R-squared:	0.124
Model:	OLS	Adj. R-squared:	0.098
Method:	Least Squares	F-statistic:	4.736
Date:	Wed, 08 Dec 2021	Prob (F-statistic):	0.00132
Time:	20:29:06	Log-Likelihood:	74.758
No. Observations:	139	AIC:	-139.5
Df Residuals:	134	BIC:	-124.8
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	-0.0323	0.031	-1.057	0.292	-0.093	0.028
VRD1	-0.0072	0.005	-1.557	0.122	-0.016	0.002
VRD2	-0.0023	0.010	-0.225	0.822	-0.022	0.018
DRD1	-0.0123	0.004	-3.262	0.001	-0.020	-0.005
PROMPTITUDE	0.0003	0.000	0.705	0.482	-0.000	0.001

Omnibus:	31.182	Durbin-Watson:	1.822
Prob(Omnibus):	0.000	Jarque-Bera (JB):	51.748
Skew:	1.074	Prob(JB):	5.80e-12
Kurtosis:	5.080	Cond. No.	224.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

To validate the hypothesis of the earlier onset and a faster increasing rate of vaccination, which possibly correlates with a lower death rate over time, we build an OLS regression model to find the correlation between the independent variables: VRD1(vaccination rate) and PROMPTITUDE (days since first vaccination onset date) with the dependent variable: DRD1 (death rate). We see that the R-squared score is moderately high with $$R^2 = 0.322$$ which corresponds only 32.2% of the variation of Generosity could be explained by these independent variables.

In the summary, we can see that the p-value for PROMPTITUDE is less than $$\alpha = 0.01$$ This means that it is statistically significant to conclude that there is a correlation between PROMPTITUDE and DRD1.

However, the p-value for VRD1 is greater than $$\alpha = 0.01$$ Thus we can’t conclude that there exists a correlation between VRD1 and DRD1.

outcome, predictors = patsy.dmatrices(
    "DRD1 ~ VRD1 + PROMPTITUDE", features)
model = sm.OLS(outcome, predictors)

results = model.fit()
results.summary()

OLS Regression Results

Dep. Variable:	DRD1	R-squared:	0.322
Model:	OLS	Adj. R-squared:	0.312
Method:	Least Squares	F-statistic:	32.27
Date:	Wed, 08 Dec 2021	Prob (F-statistic):	3.39e-12
Time:	20:29:06	Log-Likelihood:	-362.35
No. Observations:	139	AIC:	730.7
Df Residuals:	136	BIC:	739.5
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.6590	0.543	4.898	0.000	1.585	3.732
VRD1	-0.2104	0.096	-2.200	0.029	-0.400	-0.021
PROMPTITUDE	-0.0368	0.006	-5.727	0.000	-0.050	-0.024

Omnibus:	4.281	Durbin-Watson:	2.078
Prob(Omnibus):	0.118	Jarque-Bera (JB):	2.685
Skew:	-0.134	Prob(JB):	0.261
Kurtosis:	2.374	Cond. No.	170.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Given that the R-squared of the OLS model using healthy life expectancy is the highest of all, we decide to let this metric become the “happiness score” that we have been proposing at the beginning of the project. Therefore, we want to build our regression model based on this metric. Considering that our four independent variables: VRD1, VRD2, DRD1, and PROMPTITUDE are not in the same magnitude and the fact that they contain outliers (as illustrated in EDA), we decide to standardize these features using RobustScaler, which scales the data according to the quantile range with 1st quartile (25th quantile) and the 3rd quartile (75th quantile). We selected SVR, LinearRegression, and RandomForestRegressor as our models, and each of which represents a unique paradigm to do a regression task. SVR is a support-vector based regressor that is able to map the original features into higher dimensions and finds a linear function that representing data in a margin of error; Linear regression is a simple linear model that uses an analytical solution to find model parameters based on training data (i.e. X@w=Y); on the other hand, random forest regressor is a rule-based model that tries to find various numbers of decision trees, and each of which minimizes the entropy on a subsample of training data. Our experimentation results show that the RandomForestRegressor gives us the best R-squared score of 0.746, where as Linear Regressor or SVR did not perform as well as the Random Forest Regressor. However, since our training data and validation data are both small in size, these results might still be unstable and could differ if a different split strategy is adapted or more data is used (unfortunately, there are only limited numbers of countries in the entire world, so it’s essentially a few shot learning problem, and we believe that it’s unethical to train such a model with arbitrary generated/augmented data).

# we have used RobustScaler() to build our model to prevent outliers from 
X, y = RobustScaler().fit_transform(features[['VRD1', 'VRD2', 'DRD1', 'PROMPTITUDE']]), \
        features.Healthy_life_expectancy

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# set our models
models = [
    SVR().fit(X_train, y_train),
    LinearRegression().fit(X_train, y_train),
    RandomForestRegressor(random_state=42).fit(X_train, y_train),
]

init_results = {str(type(model).__name__): model.score(X_test, y_test) for model in models}
init_results

{'SVR': 0.6249987361536417,
 'LinearRegression': 0.6931543731709369,
 'RandomForestRegressor': 0.7409978325189819}

Latent Variable Modeling

Because we observed in the EDA that regional indicator is a key factor in determining an approximate range for days since earliest onset (i.e. promptitude) and healthy life expectancy (see figure 4), we believe that some underlying variables exist such that data points belonging to any underlying (i.e. latent) variable follows some paramterized distributions. Here, we make the assumption that these latent variables are all parameterized by gaussians (there are better ways to approximate a parameterized distribution, but due to the scope of the class, we think assuming them to be gaussians is sufficient to make the case, even for extra credit). Simply saying, we wonder if we can mine the regional indicators without explicitly using them.

Therefore, we will use a Gaussian Mixture Model to fit and predict the cluster labels of our data. To validate that these cluster labels actually do resemble regional indicators, we used normalized mutual information score to make comparisons on comparing the mutual information score between regional indicator labels and clustering labels, and the mutual information score between regional indicator labels and randomly assigned labels. Results show significantly higher normalized mutual information score when it comes to comparing clustering labels with actual regional indicator labels in any numbers of components; the highest normalized information score achieves at 6 components. At this stage, we are sure that using a gaussian mixture model does approximately cluster data points with regard to their respective regional indicators, but we need to dig a deeper into the results and see why 6 components work better than 10 components (the regional indicators have a total of 10 distinct categories). To analyze this, we used the TSNE to visualize the difference between clustering labels and actual regional indicator labels.

latent_stats = {
    'Number_of_Components': [],
    'NMI_Score_on_Dummy': [],
    'NMI_Score_on_GMM': [],
}
for i in range(1, df['Regional indicator'].nunique()+1):
    np.random.seed(42)
    latent_stats['Number_of_Components'].append(i)
    latent_stats['NMI_Score_on_GMM'].append(
        normalized_mutual_info_score(df['Regional indicator'].values, 
                               GaussianMixture(i).fit_predict(X)),
    )
    latent_stats['NMI_Score_on_Dummy'].append(
        normalized_mutual_info_score(df['Regional indicator'].values, 
                               np.random.randint(i, size=len(y)))
    )
latent_stats = pd.DataFrame(latent_stats)

plt.rcParams['figure.figsize'] = [9.8, 5.5]
f, ax = plt.subplots()
latent_stats.set_index('Number_of_Components').plot(kind='bar', ax=ax, xlabel='Number of Components', 
                title='Normalized Mutual Information Score on Regional Indicator Inference with GMM',
                ylabel='Normalized Mutual Information Score');

This TSNE result gives as sufficient insights into why having 6 components work better than having 10 components in terms of normalized mutual information score. As we can see, almost all data points assigned to cluster 1 belong to either Western Europe and Central and Eastern Europe (with two exceptions, one from Southeast Asia, and the other from North America and ANZ). On the other hand, almost all data assigned to cluster 0 mostly belong to Middle East and North Africa and Sub-Saharan Africa. Other clustering labels don't show significant correlations with specific regional indicators, but cluster 0 and 1 are themselves sufficient to show that these gaussians do reconstruct information in terms of regional indicators.

np.random.seed(42)
coordinates = TSNE(n_components=2).fit_transform(X)
latent_cat = GaussianMixture(6).fit_predict(X)
f, ax = plt.subplots()
sns.scatterplot(
    x=coordinates[:,0], 
    y=coordinates[:,1], 
    ax=ax, 
    hue=latent_cat, 
    style=df['Regional indicator'].values, 
    palette='tab10',
)
ax.set_title('Visualization on Relationships Between Latent Modeling results and Actual Regional Indicator via TSNE')
ax.legend(bbox_to_anchor=(1.05, 1), ncol=2, fontsize='small');

Now, after we know the fact that using a gaussian mixture model for our independent variables (i.e. VRD1, VRD2, DRD1, PROMPTITUDE) gives us underlying information on regional indicators, we wonder if the addition of thse clustering labels improve the performance of our models or not. As such, we decide to one-hot encode the clustering labels from gaussian mixture results and add these encodings as part of the data input. The below results and the figure show that the addition of latent variable modeling improves all three models we have used previously. For SVR and Linear Regression, each clustering label serve as a unique intercept for that serves all data points having that label, and for Random Forest Regressor, each clustering label serves as a decision that helps each tree in the model further reduce the entropy and makes better decisions.

np.random.seed(42)
z = OneHotEncoder(sparse=False).fit_transform(
    pd.DataFrame(GaussianMixture(6).fit_predict(X)), )
X_with_latent = np.concatenate([X, z], axis=1)

X_train, X_test, y_train, y_test = train_test_split(X_with_latent, y, test_size=0.33, random_state=42)

models = [
    SVR().fit(X_train, y_train),
    LinearRegression().fit(X_train, y_train),
    RandomForestRegressor(random_state=42).fit(X_train, y_train),
]

latent_results = {str(type(model).__name__): model.score(X_test, y_test) for model in models}
latent_results

{'SVR': 0.6186086444279955,
 'LinearRegression': 0.6805391872165707,
 'RandomForestRegressor': 0.7459539079240782}

plt.rcParams['figure.figsize'] = [9.8, 5.5]
f, ax = plt.subplots()
comparison = pd.concat([pd.Series(init_results), pd.Series(latent_results)], axis=1)
comparison.columns = ['Model_Trained_Without_Z', 'Model_Trained_With_Z']
comparison.plot(kind='barh', ax=ax, rot=70, title='Model Performance Comparison on Test Set');
ax.set_xlabel('R2 on Test Set');

Based on the EDA and the above statistical analysis results, we derive the following key takeaways:

1. Globally, a faster increasing rate of vaccination doesn't necessarily correlate with a lower death rate over time. As we see from figure 7 (the boxplot), the new death rate doesn't show a decreasing trend overall when we increase the time span.
2. Locally, an earlier onset date of vaccination brings a decreasing trend of new average death rate over time more likely on developed regions, while ironically, an increasing trend of new average death rate over time is observed on developing regions. While it's intuitive to understand the trend happening in developed regions, we believe the reason that the trend is reversed in developing countries is because the virus transmitted to these areas in large scale at a later time, and the statistics, especially in terms of calculating infection and death rate, were not accurate enough when the virus just broke out. These two reasons possibly caused the reversal of correlation when it comes to developing countries. As a future scope, more works are needed to explore the authenticity of such claims.
3. Among various "happiness" metrics, social support and healthy life expectancy show high correlation with our variables (i.e. First two principal components of average new vaccination rate, first principal components of average new death rate, and promptitude), while generosity and perception of correpution show low correlation with our varibles.
4. Among happiness metrics that show significant correlations, the major features being used by the model in terms of p-values come from average new vaccination rate and average new death rate. An insignificant p-value is found for promptitude (i.e. days since earlist onset) for the model under our context.

Ethics & Privacy

Data collection

• We need to make sure that data collectors have informed consent from the participants while they were collecting data. Our dataset contains data where the smallest unit is statistics from individual countries instead of individual people, so we don't expect anything extracted from this dataset to incur ethical issues or violate privacy. However, the data collection process from individuals in countries may have some issues in ethics/privacy, but we did not know the details on their data collections process, therefore would not comment more on that.

• We also need to make sure our data is as unbiased as possible. We are not worried about the sampling method because most of our data were collected from governmental public sources and merged on Kaggle. The one dataset that we need to pay more attention to is the happy score data set. Since it is a somewhat subjective measurement, we need to make sure that the data is unbiased and the sampling is truly random in order to achieve the best prediction.

• Another data collection ethical consideration is that we need to limit the exposure of PII so that we could protect participants’ privacy and anonymity. However, it is NOT our concern because all of our datasets don’t contain Personal Identifiable Information (PII). It is also impossible to extract any individual information for a dataset with a whole country as its unit.

Data storage

• Data storage should NOT be an issue, since it is from open-source websites. However, we need to pull our dataset from Kaggle frequently to ensure it is the most up-to-date version.

Analysis

• We will respect our data. No matter what the result from our data is, we won’t manipulate the data in order to make it fully support our hypotheses. If there doesn’t exist any association between vaccination rates, death rates, and happiness score rates. We won’t modify our data to create that association. If this situation turns out to be true, then we should explore some association between happiness score rate and other variables.

• In terms of data visualization, we need to make sure that we present our data with honesty and integrity. We can’t exaggerate some associations, and we can’t hide some of the differences while making them look negligible. We also can’t enlarge the scale to make something really small look big enough.

• We should also minimize the exposure of personally identifiable information(PII) when making the analyses. In our case, this is not our concern.

• We need to address the following questions before running our hypothesis test.

  • Did all people answer the survey questions faithfully?
  • There might be some unfaithful respondents, so how should we filter them out?
  • Did the government interfere with the public attitude towards the survey questions?
  • With government interference, there could exist potential inflation in people’s happiness scores. People might seem to be happier than they truly are.
  • Did all people in a given country have access to the survey?
    • For example, if the survey questions were distributed on some international website, not all Chinese people have access to it due to the firewall blockage. Additionally, some people in underdeveloped countries might not even have internet access.
  • Does the survey serve some political purposes?
    • For example, if the survey was given by social media from a western country that sought to degrade eastern countries, it is essentially unfaithful. These are all questions we need to address in order to be as unbiased as possible.

Modeling

• Proxy discrimination: We will ensure that we are using variables that are not discriminatory so that we can protect fairness among groups, such as different gender, race, and job titles.This should not be an issue since our dataset doesn’t contain any above discriminatory variables.

• Fairness across groups: In our case, we should test our model results for fairness with respect to different countries

• Explainability: Our explanation for this experiment should be precise, proper, and easy to understand.

• Metric selection: We should use appropriate metrics to make our results more understandable and explain any limitations or shortcomings.

• Communicate bias: We should also list limitations and potential improvements at the end of our research. One limitation is that some vaccines require two shots, but some only need one; the shot difference might also contribute to the different vaccination rates.

Reproducibility and replicability

• After we finalize our report, we will post our analysis together with our source to some public sites such as github. Thus, our analysis can be subjected to public discernment. Together with our code and analysis procedure, others can easily reproduce our analysis. However, other data analysts might reach a different conclusion from ours, since new records on happiness scores or vaccination will come. Thus, the population we analyze will not be constant. Fill in your ethics & privacy discussion here

Conclusion & Discussion

Here we would like to reinforce our question:

How the onset of vaccination, the vaccination rates, and the death rate in a country are related to the happiness score of that country?

And the hypothesis:

An earlier onset and an increasing rate of vaccination, which possibly correlates with a lower death rate over time, result in a potentially higher happiness score.

We would like to make a comprehensive conclusion based on all the above analysis: while an increasing average new vaccination rates don't generally correlate with a decreasing average new death rates, the onset of vaccination does have a negative relationship with the average new death rates in developed countries and a positive relationship with the average new death rates in developing countries. When all three factors are taken into account, they have high correlation with two metrics of happiness score, namely social support and healthy life and expectancy, and low correlation with the other two metrics of happiness score, namely generosity and perception of corruption. We cannot derive a conclusion from the coefficient of the variables in our analysis process because independent variables have gone through PCA and standardization, which makes hard to interpret the actual meaning of coefficient. However, we can possibly still be able to observe from figures in the EDA section that the average new vaccination rates and the average new death rate positively correlate with two metrics of happiness score that have a higher correlation with all our indepdndent variables, and the number of days since the country that has the earliest onset has a negative correlation with these two highly-correlated metrics of happiness score.

We would also talk about the limitations in this project. In particular, we did not take the effects of different COVID-19 varients, different brands of vaccines, different degree of general precautions for protecting themselves against the virus, and different statistical precision in counting the number of vaccinations and deaths each day among different countries. These four differences can strongly bias our conclusion and yield some unexpected results. For instance, if a developing country had a poor surveillance system in counting the number of deaths caused by COVID-19 initially but improved significantly in the later, we would likely to see an increasing trend in average new death rate as we increase the time span despite that we also see an increasing trend in average new vaccination rates. On the other hand, if a country started vaccination before the virus gets massively transmitted, but later the virus exponentially transmitted, we will also likely to see the same pattern (i.e. a positive correlation with average new vaccination rate and average new death rate across different time spans). Finally, we assumed that countries reported their data in vaccination statistics and death statistics regarding COVID-19 are faithful. In reality, there still exists the probablity where governments report fake data to the WHO for some reasons, which could also bias our conclusion. Again, our conclusion was based on the analysis of all data we collected from Kaggle - if more factors are taken into account and the data is more faithful, it's yet not unexpected to possibly see an opposite conclusion.

Team Contributions

• Colin Wang
  • Formulation of project, all source code, some text analysis.
• Luning Yang
  • Inline comments, text analysis.
• Weiyue Li
  • Inline comments, text analysis.
• Yuru Zhou
  • Inline comments, text analysis.

We don't specify teammates to concentrate on specific sections. That said, all of us contribute to all sections, and all of us work together for every checkpoint. Each of us has considerable efforts in building this project.

Appendix: Team Expectations

• Respect each other in terms of different ideas, different experience on working on a group project, and so on.
• Effective and efficient communication.
• Working towards the same goal: getting out of this course with a project that we are proud of!

---

Appendix: Project Timeline

Meeting Date	Meeting Time	Completed Before Meeting	Discuss at Meeting
10/20	5 PM	Read & Think about COGS 108 expectations; brainstorm topics/questions	Determine best form of communication; Discuss and decide on final project topic; discuss hypothesis; begin background research
10/21	5 PM	Do background research on topic	Discuss ideal dataset(s) and ethics; draft project proposal
10/23	10 PM	Edit, finalize, and submit proposal; Search for datasets	Discuss Wrangling and possible analytical approaches; Assign group members to lead each specific part
11/15	6 PM	Import & Wrangle Data; EDA	Review/Edit wrangling/EDA; Discuss Analysis Plan; Submit Checkpoint #1: Data*
11/19	5 PM	Finalize wrangling/EDA; Begin Analysis	Discuss/edit Analysis; Submit Checkpoint #2: EDA*
11/30	5 PM	Complete analysis; Draft results/conclusion/discussion	Discuss/edit full project
12/1	5PM	Finalize project	Turn in Final Project & Group Project Surveys